и 
умножаются по правилу:
ОБ АНАЛИТИЧЕСКОЙ ЭЛЕКТРОДИНАМИКЕ
А. Н. Аверкин
В рамках существующего взгляда на классическую электродинамику как материализацию теории аналитических функций некоторого гиперкомплексного переменного оказывается возможным придать электродинамике определенное геометрическое истолкование. Для этого, однако, следует допустить, что расстояния в пространстве-времени не обязательно удовлетворяют так называемой аксиоме Архимеда, т. е., что алгебра пространства-времени является неархимедовой. Кроме того, получены, как представляется, некоторые данные о природе электрических зарядов.
В работах
[1, 2 и др.] классическая электродинамика, по существу, рассматривается как материализация теории аналитических функций бикватернионного переменного (бикватернионами называют кватернионы определенные над полем комплексных чисел). Определенным недостатком алгебры кватернионов для указанных приложений является то, что комплексная мнимая единица по своим коммутационным свойствам отличается от таковых кватернионных единиц. Это приводит, в частности, к тому, что “квадрат модуля бикватерниона”, соответствующего, например, электромагнитному полю, оказывается комплексным числом. Результаты этой работы могут быть получены, по-видимому, в рамках алгебры кватернионов, однако, в связи с вышесказанным, представляется более естественным использовать для описания электродинамики несколько иную алгебру, которую будем называть алгеброй астральных чисел. Эту алгебру, родственную алгебре октав, можно получить, воспользовавшись процедурой удвоения гиперкомплексных алгебр Кэли-Диксона при помощи “гипердействительной единицы” l, или, говоря более определенно, если a, b, c и d — кватернионы, то представители астральной алгебры и умножаются по правилу:
Очевидно, что алгебра астральных чисел, как и алгебра октав, является неассоциатив
ной, поэтому, чтобы писать меньше скобок, условимся порядок сомножителей
называть нормальным и записывать такие произведения без скобок.
Из формулы (1) легко получить правила обращения с астральной единицей l. Если a и b — кватернионы, то
Будучи неассоциативной, алгебра астральных чисел сохраняет, тем не менее, подобно алгебре октав, свойство альтернативности умножения, которое, в самом общем виде, означает, что произведение любого числа астральных сомножителей, составленное только из двух разных чисел (и чисел им сопряженных), не зависит от последовательности проведения умножений и, следовательно, может быть записано без скобок. Из этого свойства астральных чисел сразу следует так называемое “тождество восьми квадратов”:
В дальнейшем будем обозначать 
и называть это действительное число мерой астрального числа.
Важное отличие алгебры астральных чисел от таковой октав заключается в том, что множество астральных чисел, у которых мера равна нулю, состоит из более чем одного числа. Астральные числа с нулевой мерой будем называть, как это принято в других алгебрах, идеальными.
Если переобозначить астральные единицы соответствующим образом, то четырехмерные объекты a и b, образующие астральное число 
, будут обладать структурой
но отличаться от кватернионов правилами умножения. Соответствующая таблица умножения будет иметь вид:
Все единицы i, j, k и l антикоммутируют между собой. Присвоим таким объектом название эфирных объектов, а произведению эфирного объекта на астральную единицу l — ментального объекта и впредь будем записывать астральные числа в виде суммы эфирной и ментальной частей. Эфирные объекты, сами по себе, не образуют какой-либо алгебры, удобно, однако, пользоваться терминами – эфирные и ментальные числа, подразумевая под этим астральные гиперкомплексные числа, состоящие только из эфирных или ментальных объектов.
Если ввести симметричное произведение эфирных чисел:
где 
– скалярное произведение соответствующих четырехмерных векторов, а также антисимметричное произведение — 
то произведение эфирных чисел можно кратко записать как
Легко проверить, что, если a и b – эфирные числа, то для них формулы (1) и (2) справедливы так же, как и для кватернионов.
Пусть эфирное число одновременно является и вектором, т. е. его компоненты при преобразовании координат преобразуются так же, как и компоненты 4-вектора. В этом случае, как известно, лоренцевское преобразование 4-вектора очень удобно описывать на языке бикватернионов. Для проведения таких преобразований мы, вместо того, чтобы ставить астральному числу в соответствие бикватернион, определим ассоциативное умножение астральных чисел, что, в общем, то же самое:
т. е. при выполнении ассоциативного умножения астральная единица ведет себя как единица мнимая, коммутирующая со всеми эфирными единицами. Во избежание двусмысленностей будем считать, что ментальная часть, как астральных сомножителей, так и результата ассоциативного умножения имеет вид al (но не 
; а — эфирное число).
При помощи ассоциативного умножения преобразование эфирного числа а можно описать формулой:
где астральному числу 
соответствует число 
. Если мера числа q не равна единице, то это число не только осуществляет лоренцево преобразование эфира, т. е. пространства эфирных чисел, но и однородное его сжатие. Унитарное число q имеет семь независимых параметров, тогда как для описания лоренцевского преобразования эфира достаточно шести. Поэтому мы можем наложить на компоненты дополнительное условие, в качестве какового примем, что 
Это означает, что любое лоренцево преобразование эфира можно понимать как последовательное выполнение пространственного вращения, представленного кватернионом, и преобразования Лоренца в узком смысле, представленного эфирным числом.
Заканчивая главу, отметим, что, если астральное число 
ортогонально, то задаваемое им преобразование (3) можно записать и без помощи ассоциативного умножения, т.
где 
Введем дифференциальный оператор, про который условимся, что он действует на соответствующие функции астрального аргумента слева:
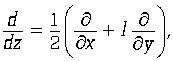
где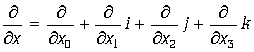 
и 
— соответственно. Коэффициент
введен в этот оператор для того, чтобы в частном случае он переходил в оператор дифференцирования аналитической функции комплексного переменного. Определение аналитической (точнее, леворегулярной) функции 
астрального аргумента является обобщением определения аналитических функций комплексного и кватернионного [3] аргументов, годным для любого гиперкомплексного переменного:
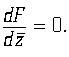
Мы, однако, не будем рассматривать здесь аналитические функции астрального переменного общего вида, но ограничимся такими функциями, у которых 
; иначе говоря, мы будем иметь дело с функциями, которые зависят только от аргумента 
. Этот аргумент соответствует точкам четырехмерной эфирной гиперплоскости, лежащей в восьмимерном пространстве астральных чисел. Будем называть такие функции — аналитическими функциями эфирного переменного. Эти функции удовлетворяют условию аналитичности
Если аналитическую функцию 
записать в виде:
то восьмимерному уравнению (4) будет соответствовать следующая система
уравнений:
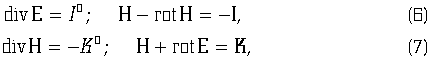
где точкой обозначено дифференцирование по 
. Эти уравнения внешне совпадают с уравнениями Максвелла при наличии магнитных и электрических зарядов-токов, образующих единство, которое можно назвать астральным током. Если обозначить этот ток как L, то
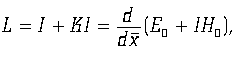
или более подробно:
Уравнения (4 – 7), выражающие условия
аналитичности, имеют несколько иной смысл, чем соответствующие уравнения Максвелла. Дело в том, что в последних уравнениях заряды и токи, коль скоро они удовлетворяют уравнению непрерывности, являются заданными функциями. Очевидно, что заряды и токи, входящие в условия аналитичности, удовлетворяют уравнениям непрерывности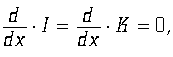
однако, выражаясь через нуль-поля 
как через потенциалы, они сами определяются через то или иное решение уравнений (6, 7). Кроме обычных решений в виде поперечных электромагнитных волн — в этом случае астральный ток L равен нулю — эти уравнения имеют решения, которые мы назовем продольными электрическими и магнитными волнами. Они имеют вид:
где f и g — некоторые действительные функции скалярного аргумента 
, а q — эфирное число, удовлетворяющее равенству 
. Отметим, что все решения в виде волн, как поперечных, так и продольных, иначе говоря, решения аналитичные во всех точках пространства-времени являются идеальными функциями эфирного аргумента, т. е. их мера везде равна нулю.
Аналитические функции эфирного переменного можно выразить через потенциал A, удовлетворяющий уравнению д’Аламбера:
В общем случае потенциал А является астральнозначной функцией эфирного переменного, однако, — по причинам, которые будут ясны из дальнейшего — потенциал А можно считать эфирным, т. е. 
В этом случае астральное поле F выражается через эфирный потенциал следующим образом:
или, расписывая по составляющим,
Очевидно, что в случае применения эфирного потенциала ментальная составляющая астрального тока равна нулю. Если считать, что компоненты эфирного потенциала образуют 4-вектор, т. е., что при лоренцевском преобразовании координат (3) потенциал A преобразуется по этой же формуле, то преобразование астрального поля осуществляется по формуле
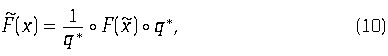
где q — обязательно ортогональное астральное число. При этом условии, формула (10) соответствует известному [4]
преобразованию электромагнитного поля к движущейся системе отсчета (нуль-поле
следует, естественно, считать скаляром).
В связи с преобразованием (10) отметим, что термин электрическая продольная волна является несколько условным. Если перейти от той системы отсчета, в которой распространяется продольная волна, к системе, движущейся с некоторой скоростью в направлении перпендикулярном волновому вектору этой волны
, то, наряду с электрическим полем Е, появится и перпендикулярное этому полю некоторое магнитное поле Н. Это обстоятельство означает, что в произвольной инерциальной системе отсчета продольная электрическая волна сопровождается сопутствующей поперечной волной, т. е. является, как говорят, ТМ-волной. Таким образом, продольная электрическая волна отличается от обычной электромагнитной волны тем, что ее инвариант не равен нулю:
При наличии продольных волн калибровочная инвариантность электромагнитного поля сводится к тому, что оно не изменяется при замене
где
j — скалярная функция, удовлетворяющая уравнению д’Аламбера. Если мы имеем систему произвольно движущихся зарядов, то соответствующие запаздывающие потенциалы автоматически, как известно [4], удовлетворяют калибровке Лоренца: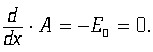
Этот факт означает, что никакая система электрических зарядов не может испустить продольную электрическую волну; он означает также, что эта система не может и поглощать продольные волны. Это не означает, конечно, что продольные электрические волны не будут когда-либо наделены физическим смыслом. Таким образом, принятие калибровки Лоренца просто означает, что мы исключаем из рассмотрения продольные электрические волны.
Для перехода от электродинамики, сформулированной на языке аналитических функций, к электродинамике в тензорных обозначениях эфирным объектам 
следует сопоставить контравариантные 4-векторы 
, а сопряженным объектам 
— соответствующие ковариантные. Тензор электромагнитного поля 
состоит теперь из суммы двух тензоров: симметричного – 
и антисимметричного – 
. Связь этого тензора с аналитической функцией F удобно определить в виде:
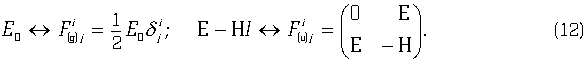
3. Геометрический смысл аналитических функций
Рассмотрим преобразование эфирного пространства вида
такое что каждая его точка сдвигается на малую величину w(x). Соответственно этому преобразованию окрестность каждой точки эфира деформируется следующим образом:
где 
. Тензор 
, ассоциированный тензору
, можно представить в виде совокупности симметричного и антисимметричного тензоров:
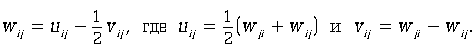
В свою очередь тензор 
, который можно назвать тензором деформации эфира, запишем как
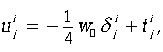
где скаляр 
. Первое слагаемое в такой записи тензора деформации соответствует однородному сжатию эфира, а тензор 
, след которого равен нулю, можно назвать тензором деформации сдвига.
Что касается тензора 
, то он осуществляет малый поворот окрестности точки х, т. е. ее лоренцево преобразование. Это видно хотя бы из того, что приращение вектора 
, которое в этом случае записывается как
в силу антисимметричности тензора , ортогонально самому вектору 
:
Сопоставим теперь тензору
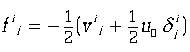
(этот тензор можно назвать тензором релятивистски-конформной составляющей деформации эфира) функцию 
согласно соотношениям (12). Эта функция выражается через деформацию w подобно тому, как астральное поле 
— через эфирный потенциал А (см. формулу (9)). Если же потребовать, чтобы деформация w удовлетворяла уравнению д’Аламбера или, что то же самое
:
где с – скорость света, возникающая здесь из-за того, что в элемент четырехмерного объема 
входит не время, но координата 
, то мы могли бы предположить, что аналитическая функция 
пропорциональна соответствующему электромагнитному полю .
Такое отождествление встречает, однако, препятствия следующего рода. Когда мы говорим, что деформация w является малой, то это, с физической точки зрения, означает существование некоторой фундаментальной длины
l, при этом следует считать, что все компоненты деформации
. В свою очередь длина 
должна быть достаточно малой, чтобы быть необнаружимой в рамках известных экспериментальных данных. Если же безразмерная деформация 
, то вся теория делается нелинейной. Кроме того, наличие деформации эфира приводило бы к тому, что соответствующая этой деформации система отсчета являлась бы инерциальной, и можно было бы ожидать, при наличии электромагнитного поля, появления специфических сил инерции.
С другой стороны, теория функций эфирного переменного, с которой мы пытаемся отождествить физическую теорию электромагнитных явлений, является строго определенной математической дисциплиной, уравнения которой линейны и не содержат в себе каких-либо ограничений на величину компонент эфирного потенциала. Она указывает лишь, что, в связи с тензорным характером преобразования компонент аналитической функции
Существование таких чисел еще недавно представлялось бы абсурдным, однако, относительно недавно, была безупречно, с математической точки зрения, построена теория числовой оси, в которой поле действительных чисел расширяется до поля так называемых гипердействительных чисел. При этом пришлось отказаться от аксиомы Архимеда, верной для всех действительных чисел, отличных от нуля. Эта аксиома утверждает, что для любых двух отрезков а и b можно меньший из них (а) отложить столько раз, чтобы в сумме получить отрезок, по длине превосходящий больший (b). Именно среди гипердействительных чисел встречаются отличные от нуля числа, не удовлетворяющие аксиоме Архимеда, — они то и называются бесконечно малыми числами.
Таким образом, мы будем считать, что теория аналитических функций эфирного переменного имеет дело с инфинитезимальными преобразованиями эфирного пространства. Отметим, что при этом у нас нет необходимости специально определять компоненты потенциала w как 4-вектор: если этот потенциал бесконечно мал, то он автоматически является вектором. Математический анализ, построенный на основе нового представления об устройстве числового поля, — он называется нестандартным анализом [6, 7]
— является формализацией соответствующих воззрений Лейбница и интуитивно представляется более естественным, чем стандартный; во всяком случае, в этом анализе понятие дифференциала, в отличие от анализа Ньютона-Коши, имеет вполне ясный смысл.Поскольку энергия электромагнитного поля является отнюдь не бесконечно малой величиной (это означает, что эфир является настолько “жесткой материей”, что его бесконечно малые деформации уже приводят к возникновению конечной плотности энергии), то мы должны соответствующим образом нормировать инфинитезимальное действие s[w].
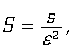
где
e – “бесконечно малая константа” соответствующей размерности. Если положить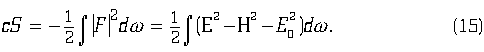
, то действие S можно записать в более привычном виде:
Отметим, между прочим, что появление коэффициента равного двум в выражении деформации w через потенциал А отвечает тому факту, что, с математической точки, зрения было бы естественным сохранить коэффициент равный 
в определении оператора эфирного дифференцирования 
, при этом, однако, электромагнитное поле выражалось бы через векторный потенциал нетрадиционным образом; подобный смысл имеет и появление в этом выражении отрицательного знака.
Таким образом, мы видим, что вполне логично поставить в соответствие аналитической функции эфирного переменного
релятивистски-конформную составляющую инфинитезимальной деформации пространства-времени. При этом относительное изменение элементарного объема, вызванное его однородным сжатием, определяется выражением 
. Кроме того, окрестность точки х приобретает бесконечно малую скорость 
и поворачивается на угол q 
. Отметим еще, что, если деформация w выражается через скалярную функцию 
, являющуюся решением уравнения д’Аламбера, как через потенциал, то такая деформация с необходимостью оказывается деформацией сдвига. Таким образом, функцию j , осуществляющую калибровочное преобразование эфирного потенциала (11), можно назвать потенциалом деформации сдвига, поскольку именно она определяет вид соответствующего тензора 
.
*
Кроме функций в виде совокупности тех или иных волн — такие функции аналитичны во всем пространстве-времени — уравнения (4 – 7) имеют и другие решения. Эти решения аналитичны лишь в тех областях эфира, что не содержат особых точек, т. е. точек, в которых условия аналитичности не выполняются. Представляется, что, исходя из принципа инфинитезимальности деформации эфира, можно получить определенную информацию о характере этих особенностей аналитических функций.
Определение аналитических функций эфирного переменного не содержит, само по себе, требования бесконечной малости деформаций эфира и, следовательно, самих аналитических функций. Чтобы явно учесть это обстоятельство, скажем, что деформация эфира определяется экстремумом функционала (14) при том условии, что
где
l – произвольная, но конечная длина. Поскольку инфинитезимальная деформация, с точки зрения алгебры действительных чисел, равна нулю то оказывается возможным сформулировать эту задачу на условный экстремум функционала s[w] при помощи соответствующих множителей Лагранжа [5]. Иначе говоря, деформация эфира должна доставлять экстремум функционалу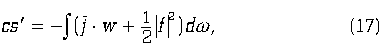
где функции 
удовлетворяют условию
Поскольку в формуле (17) мера аналитической функции f является величиной второго порядка малости по сравнению с компонентами самой деформации, т. е. 
, то и интеграл
должен иметь тот же порядок малости. Это означает, что та область эфира, в которой эфирнозначная функция 
отлична от нуля, должна иметь бесконечно малый объем. В связи с этим естественно считать, что эта область представляет собой бесконечно тонкую двумерную мембрану, форма и пространственное расположение которой зависят от времени. Иначе говоря, множество точек, в которых компоненты функции отличны от нуля, образуют область, описываемую четырьмя параметрами 
(т. е. 
); при этом можно считать, что 
, а один из оставшихся параметров, например 
, принимает лишь бесконечно малые значения. Очевидно, что поверхность, соответствующая этой мембране, должна быть замкнутой.
Положим теперь
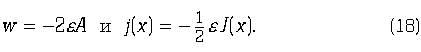
Значения, которые принимают компоненты функции 
, являются бесконечно большими, т. е., пользуясь языком нестандартного анализа, принадлежат другой галактике. Если не вникать во внутреннюю структуру мембраны, то функцию 
можно записать в виде:
где функции 
— ее можно назвать поверхностной плотностью четырехмерного тока — и 
зависят только от трех параметров 
. Подставив в функционал (17) соотношения (18), мы придем к действию сS для электромагнитного поля в присутствии зарядов, плотность лагранжиана которого имеет вид:
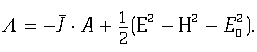
Поскольку плотность функции Лагранжа должна быть скаляром, компоненты функции 
должны преобразовываться как составляющие соответствующего контрвариантного вектора. Результатом варьирования действия с таким лагранжианом является пара уравнений Максвелла, которая отличается от уравнений (6) тем, что в них, вместо эфирного тока I, входит сумма эфирного и обычного тока J. Для того чтобы эти уравнения имели решения во всем пространстве-времени, в том числе и в точках, находящихся внутри электромагнитных мембран, четырехмерный ток 
должен удовлетворять уравнению непрерывности. Чтобы показать это, достаточно первое из уравнений (6) продифференцировать по 
, взять дивергенцию от второго из этих уравнений и из первого результата вычесть второй. При отсутствии нуль-поля и, следовательно, эфирного тока I уравнению непрерывности удовлетворяет обычный ток J.
Таким образом, мы приходим к важному результату, заключающемуся в том, что отождествление векторного потенциала с инфинитезимальной деформацией эфира автоматически приводит к появлению в лагранжиане электромагнитного поля известного члена, связанного с существованием обычных зарядов и токов. Этот результат представляется вполне естественным в том смысле, что такого рода деформация эфира не совместима с теми особенностями электромагнитного поля, которые мыслимы в том случае, если эфирный потенциал не связывать как-либо с геометрией пространства-времени. Сами по себе, уравнения Максвелла допускают, например, решения, особые точки которых представляют мультиполи различного порядка. В частности, если рассматривать электрон как точечный электрический монополь, находящийся в точке 
, то его потенциал можно записать в виде:
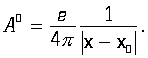
При таком потенциале соответствующая ему деформация эфира w оказывается конечной внутри окрестности точки 
, содержащей бесконечно близкие к ней точки (из уважения к Лейбницу такие окрестности в неархимедовом анализе называют монадами) — конечность же величины деформации внутри бесконечно малой окрестности противоречит условию (16), да и здравому смыслу. Отметим еще, что, в силу ненулевой толщины электромагнитной мембраны, точечный электрон топологически не может рассматриваться как предельный случай сферического электрона, т. е. состоящего из сферической заряженной мембраны, при стремлении радиуса последнего к нулю.
Механические и электромагнитные свойства полученных мембран (в первую очередь это касается существенно двумерных сил, действующих внутри мембраны и обеспечивающих стабильность электрона, — исторически эти силы называют силами Пуанкаре) не вытекают из предложенной в этой работе теории классического (неквантового) электромагнетизма. В связи с этим встает задача существенного усовершенствования теории. Мы не будем здесь делать каких-либо предположений феноменологического характера о свойствах мембран, хотя некоторые из них и могут казаться вполне естественными, Укажем лишь на то, что требование релятивистской инвариантности классического электрона, т. е. равенства его массы покоя и массы, участвующей в формировании его импульса, является недостаточным для однозначного определения свойств взаимодействия Пуанкаре.
4.Электродинамика и общая теория относительности
Наличие электрического нуль-поля естественным образом следует из предложенного для описания классической электродинамики математического формализма. Желая исключить его существование, мы должны сделать выходящее за рамки этого формализма предположение о “несжимаемости эфира”, что очень не приятно, с философской точки зрения. В связи с этим мы внимательнее рассмотрим те следствия, которые проистекают из существования этого поля.
Тензор энергии-импульса электромагнитного поля при наличии нуль-поля 
легко получить, варьируя соответствующее действие (15), записанное в произвольных криволинейных координатах, по компонентам метрического тензора 
[4]. В результате этой операции мы получим, что тензор энергии-импульса состоит из двух частей:
где 
— общеизвестный [4] тензор энергии-импульса электромагнитного поля:
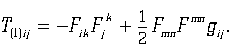
Что касается тензора 
, непосредственно связанного с существованием нуль-поля, то его можно получить из дополнительного действия с лагранжианом 
. В произвольных криволинейных координатах 4-дивер-генция вектора 
, которая равна 
, определяется выражением:
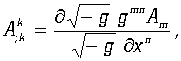
где 
есть определитель, составленный из компонент тензора 
. Выполняя стандартную процедуру, получим, что
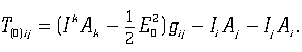
Важным свойством тензора энергии-импульса электромагнитного поля является то обстоятельство, что при наличии нуль-поля этот тензор оказывается неинвариантным по отношению к калибровочному преобразованию потенциала (11). Более того, оказывается зависящим от потенциала деформации сдвига
j и энергия-импульс электромагнитного поля, т. е интеграл от тензора
по гиперповерхности 
, содержащей трехмерное пространство.
Тот факт, что электромагнитное поле, являясь конкретным решением уравнений Максвелла (6 – 7), обладает неопределенным 4-импульсом, представляется абсурдным и дискредитирующим идею реальности нуль-поля. Однако здесь на помощь приходит, как представляется, то обстоятельство, что при наличии электрического нуль-поля след тензора энергии-импульса Т оказывается отличным от нуля:
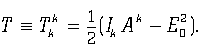
Таким образом, мы видим, что локальная (т. е. различная в разных точках) деформация однородного сжатия-растяжения эфира с необходимостью вызывает искривление пространства-времени с отличной от нуля скалярной кривизной R. Это обстоятельство позволяет, например, считать продольные электрические волны, в определенном смысле, тяжелыми — этим они отличаются как от обычных электромагнитных, так и от гравитационных волн, у которых скалярная кривизна равна нулю (для гравитационных волн это следует из вида соответствующего тензора Римана 
приведенного в [4]).
Из сказанного следует, что, сама по себе, теория электромагнетизма не является замкнутой, и мы должны определять компоненты 4-потенциала одновременно с составляющими метрического тензора непосредственно из уравнений Эйнштейна:
где гравитационная постоянная 
выбрана так, чтобы закон Ньютона имел вид:
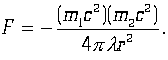
Следствием уравнения (Е) является, как известно, равенство нулю 4-дивер-генции тензора энергии-импульса материальной системы 
. Выполняя соответствующее ковариантное дифференцирование, получим:
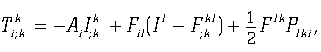
где тензор 
. Если положить 
, то автоматически выполняется соотношение
которое эквивалентно паре уравнений Максвелла (7). Уравнение же
следствием которого является уравнение непрерывности для эфирного тока I, является ковариантной записью другой пары уравнений Максвелла (6). Как мы видели уравнение (М) является дефектным, с физической точки зрения, ибо его решения не обладают, вообще говоря, определенными значениями энергии и импульса. Таким образом, уравнение (М) в общем случае не имеет смысла и должно решаться совместно с уравнением (Е) для одновременного определения составляющих метрического тензора и эфирного потенциала.
Таким образом, актуальной делается задача отыскания решения уравнения (Е), соответствующего классическому электрону. Топология солитонов, предположительно описывающих плоские заряженные мембраны, описана в разделе
“О параматерии” настоящей книги (см. рисунок).В заключение отметим, что предложенная теория является последовательно классической. Это, очевидно, связано с тем, что сама возможность построения квантового обобщения этой теории связана с созданием удовлетворительной квантовой общей теорией относительности. Кроме того, классический случай может оказаться не менее важным, чем квантовый, если в природе существуют макроскопические объекты, образованные из электромагнитных мембран
* * * *
ЛИТЕРАТУРА:
3. Fueter R., Comm. Math. Helv., 1934 - 1935, B. 7, S. 137 - 162.
4. Ландау Л. Д., Лифшиц Е. М., Теоретическая физика т. 2 (Теория поля), “Наука”, М., 1988,
стр. 90-91, 212 - 215, 349 - 360, 443.
